“Convergence of Mayer and Virial expansions and the Penrose tree-graph identity”

by Aldo Procacci, Sergio Yuhjtman.

Review by Sergio Yuhjtman

The subject belongs to the area of statistical mechanics.

Introduction

Consider a gas in a cubic box. If the interaction between the molecules is negligible, it is an ideal gas. You may be familiar with the equation of state $$pV = nRT$$ which relates pressure, volume, temperature and number of particles. For the case where the interactions are significant, the equation of state will be different. There is a model that is known to be valid since the 1930s. It describes molecules as points in a continuous (cubic) space. The interaction is determined by an energy function $V$. One interesting case is the following shape for $V$, such as the Lennard-Jones potential.

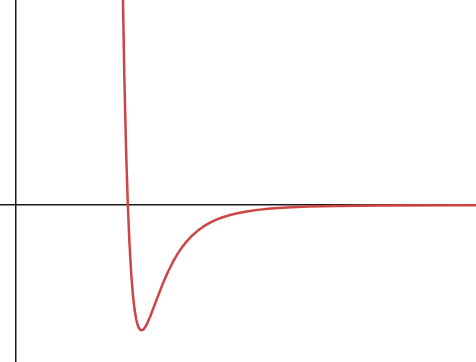
The interaction energy for a pair of particles located at $x$ and $y$ is $V(||x-y||)$. Assume we have $n$ particles in the box. According to this model, the probability density for finding the particles at specific positions $x_1, …, x_n$ depends only on the total energy $$U(\vec x) = \sum_{i \neq j} V(||x_i - x_j||) \hspace{1cm} \mbox{(total energy)}$$ The specific formula for the probability density is not crucial here, but it is the following: $$\rho(\vec x) = \frac{ e^{-\beta U(\vec x)}}{\int e^{-\beta U(\vec y)} d\vec y}$$ where $\beta = 1 /T$, and $T$ is the temperature.

Notice that configurations with larger energies are less likely to happen. If instead of fixing the number of particles we allow a variable density, the model gets slightly more complex. We introduce a parameter $\lambda > 0$, and a factor $\lambda^n$ at the probability density. At the denominator we will have every possible configuration with the corresponding factor $\lambda^{n’}$ for variable $n’$.

Some context about the problem and its physical significance

We are interested in understanding the relation between density and pressure in the case where the volume tends to infinity, the so-called “thermodynamic limit”. When the density is sufficiently low, this can be done through a technique known as “cluster expansion” or “virial expansion”. In this technique, the logarithm of the denominator of the probability density (a.k.a. the logarithm of the partition function) is expressed as a power series on $\lambda$, where the $n$-th term is a sum over connected graphs with $n$ vertices. In this way, the problem of finding the equation of state reduces to the convergence of this series, since pressure and density can be derived from it. The ideal gas corresponds to $\beta = 0$. For $\beta > 0$, if we can find a non-empty convergence region for $\lambda$, this means that the equation of state is analytic on the convergence region for $\lambda, \beta$. Thus, there is no phase transition between the ideal gas and the system at that region, implying that it is a gas.

Note: As point processes, the ideal gas is a Poisson process and the non-ideal gas is a perturbation of a Poisson process.

Some context about the solutions

This problem was first solved in 1963 by D. Ruelle and independently (or correlatedly) by O. Penrose. Later, O. Penrose developed a combinatorial method to solve special cases, namely imposing some extra restrictions to the pair potential (the energy function above). The essence of this combinatorial method is to reduce the sums over connected graphs to only the trees, which are much less. Further investigations of this method followed.

In this paper we show how to apply the tree-graph method to solve the most general form of the problem, where the pair potential only satisfies the necessary conditions of stability and temperedness. By doing so, we improve upon the classical solution from 1963, both conceptually and numerically, obtaining a stronger lower bound for the convergence radius of the series.

The key idea

“Penrose tree-graph identity” is just the following combinatorial identity:

$$\sum_{g \in \mathcal C_n} \prod_{ij \in g} (e^{-u_{ij}} - 1) = \sum_{t \in \mathcal T_n} \prod_{ij \in t} (e^{-u_{ij}} - 1) \prod_{ij \in E(t)} e^{-u_{ij}}$$

Here $\mathcal C_n$ and $\mathcal T_n$ represent respectively the set of connected graphs and trees with $n$ vertices $\{1, …, n\}$. So far we have not said what is $E(t)$.

The identity only makes sense if we have a partition scheme for the graphs. This means to have functions $\mathcal G_n \stackrel{T}{\longrightarrow} \mathcal T_n$ and $\mathcal T_n \stackrel{M}{\longrightarrow} \mathcal G_n$ such that $$T^{-1}(t) = \{ g \in \mathcal G_n / t \subset g \subset M(t) \}$$ In this case, we call $E(t) = M(t) \setminus t$ and the identity follows by applying the distributive property after appending $-1 + 1$ to the rightmost $e^{-u_{ij}}$.

This is known to be useful since the late 1960s. Our contribution in Convergence of Mayer and Virial expansions… was to realize that by choosing $T$ as the minimum spanning tree with respect to the energy, it follows the inequality

$$|\sum_{g \in \mathcal C_n} \prod_{ij \in g} (e^{-u_{ij}} - 1)| \le e^{\beta B n} \sum_{t \in \mathcal T_n} \prod_{ij \in t} (1 - e^{-|u_{ij}|})$$

where $u_{ij} = \beta V(||x_i - x_j||)$ and $B$ is the stability constant of the potential function. This inequality had been conjectured by Aldo Procacci and turned out to be true.

Unfortunately, the presentation in Convergence of Mayer and Virial expansions… is somewhat overcomplicated. Fortunately, Daniel Ueltschi’s note An improved tree-graph bound remedies this and highlights some possible straight-forward generalizations.